The Value of Trigonometry in Mathematics

Mathematics branch is well-versed as trigonometry if you aspire to become an engineer or designer. Trigonometry is “part and parcel” of higher mathematics and science.

Since trigonometry has diverse uses in practical life, it is a part of high-level math courses.

Trigonometry has diverse applications in specific parts of construction, like measurements. For example, those technologies that deal with computer graphics and medical imaging also use trigonometry.

The basic understanding of trigonometry

But, before we move forward to understand trigonometry, let us clarify the concept of a right-angled triangle. A right-angled triangle contains a single right angle, and therefore, all the sides do not maintain a similar length.

In general, the right angle is indicated by a small box placed inside one of the triangle edges. In addition, there is another angle that is pre-defined by the theta symbol.

The longest side, which lies against the right angle, is the hypotenuse.

The opposite side of the theta is known as the opposite.

The side that lies next to theta but is not the hypotenuse is the adjacent.

Students must realize the difference between the Pythagoras theorem and trigonometry. Pythagoras theorem is useful to find the length of the third side in the triangle when you know the size of its two adjacent sides. Trigonometry is valuable when we know one of the three internal angles and the length of one side.

The geometrical applications in trigonometry

Trigonometry deals with the relationship between the angles and sides of a triangle. It also includes several functions that can help determine undefined angles or sides in a triangle.

Trigonometry is crucial when calculating the angles and sides of right-angled triangles. It can help you determine the precise measurement of the angle in the right-angled triangle. If you are struggling with math problems, you must seek prompt math assignment help.

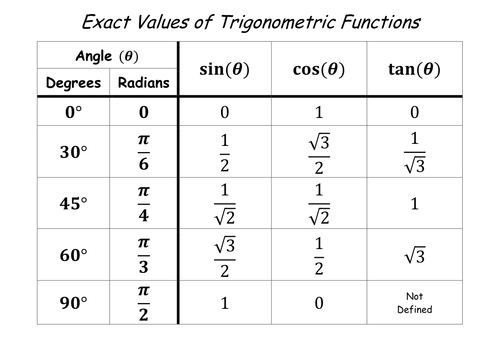
The six fundamental trigonometric ratios are – sin, cos, tan, sec, and cot.

1. sin – Perpendicular/Hypotenuse
2. cos – Base/Hypotenuse
3. tan – Perpendicular/Base
4. cot – Base/Perpendicular
5. sec – Hypotenuse/Base
6. cosec – Hypotenuse/Perpendicular

A more straightforward method to memorize the first three trigonometric ratios

One of the best ways to remember the first three ratios is by memorizing the sentence –

“Some People Have Curly Black Hair Turn Permanently Brown.”

Do you notice the first alphabet in each word of the sentence? If you gather them together, you get S, P, H, C, B, H, T, P, and B.

Now place them in like manner – Sin = Perpendicular/Hypotenuse, Cos = Base/Hypotenuse, Tan = Perpendicular/Base.

The last three, i.e., cosec, sec, and cot, are the respective inverse ratios of sin, cos, and tan.

Important – You must note that each trigonometric ratio contains an actual number without any unit.

The values of similar angles will always remain the same in trigonometric ratios.

The Analytical Use of Trigonometry

The analytical function of trigonometry uses the aforementioned trigonometric functions to assess and simplify equations. Therefore, engineering fields like electronics, mechanical engineering, and mechatronics have several applications for their analytical procedures.

Trigonometric Identities

Trigonometric identities are those equations that include an angle’s trigonometric ratios. They are also helpful in determining every trigonometric value and derivations.

Another interesting part is that both sides of the equation are similar. Therefore, you can interchange them to obtain trigonometric values.

The fundamental trigonometric identities are –

1. Sin²A + Cos²A = 1
2. 1 + tan²A = sec²A
3. 1+cot²A = cosec²A

Students must never underestimate the value and applications of trigonometry in real life. Working on these problems, in the beginning, might sound monotonous and boring. However, if they linger to it and practice it patiently and regularly, they will be rewarded.

Therefore, there is no reason to lose hope. Instead, try to build a daily habit of practicing trigonometry at home. If you fail to understand the basic concepts, do not hesitate to seek immediate Math Assignment help.

Real-life trigonometric applications

Trigonometric concepts have several real-life applications like –

1. Navigation – One of the significant real-life applications of trigonometry is its use by satellites for navigation. Trigonometry is also used in land surveying, cartography, oceanography, and naval and aviation industries.
2. Architecture – You can find the regular applications of trigonometry over mechanical structures like bridges or buildings. Trigonometry is an excellent fit in modern architecture. Engineers use basic trigonometric concepts over the blueprint the plan to make proper measurements. They can also determine the undefined sides or angles of the drawing by using trigonometry.
3. Geology – The trigonometric property – the angle of elevation – has several real-time applications across different sectors. This property can be helpful to determine the height, distance, and surface area of a structure. Geologists use the trigonometry concept – trigonometry and shadows.
4. Computer-generated Images – Trigonometry also contributes to computer imaging as it helps create complex and detailed images with a computer. For example, you will find the use of trigonometric concepts in triangulation, where complex and detailed illustrations are made.
5. Music – Are you interested in music? You will be surprised about the contribution of trigonometric applications among rhythms. The trigonometric identities – cosine and sine functions are helpful to conduct sound wave manipulations. Producers and conductors can also measure sound waves with trigonometry.

Conclusion

Trigonometry is an essential branch of mathematics with several real-life applications. You can find its relevance across multiple professions, from engineering to computers. Trigonometry is also found in navigation and music.

So, if you are pursuing trigonometry as your higher studies, be attentive in class and learn the concepts properly. All the best!